Wpisz liczbę w kropkę. Ułamki zwykłe i dziesiętne oraz operacje na nich

Ten artykuł jest o ułamki dziesiętne . Tutaj zajmiemy się zapisem dziesiętnym liczb ułamkowych, przedstawimy pojęcie ułamka dziesiętnego i podamy przykłady ułamków dziesiętnych. Następnie porozmawiajmy o cyfrach ułamków dziesiętnych, podaj nazwy cyfr. Następnie skupimy się na nieskończonych ułamkach dziesiętnych, powiedzmy o ułamkach okresowych i nieokresowych. Następnie podajemy główne akcje z ułamkami dziesiętnymi. Podsumowując, ustalamy pozycję ułamków dziesiętnych na promieniu współrzędnych.

Nawigacja po stronach.

Zapis dziesiętny liczby ułamkowej

Czytanie ułamków dziesiętnych

Powiedzmy kilka słów o zasadach odczytywania ułamków dziesiętnych.

Ułamki dziesiętne odpowiadające poprawnym wspólne ułamki, są odczytywane w taki sam sposób jak te zwykłe ułamki, tylko „zero całości” jest dodawane wcześniej. Na przykład ułamek dziesiętny 0,12 odpowiada zwykłemu ułamkowi 12/100 (czytuje „dwanaście setnych”), dlatego 0,12 jest czytane jako „dwunaście setnych punktów zerowych”.

Ułamki dziesiętne, które odpowiadają liczbom mieszanym, czyta się dokładnie w taki sam sposób, jak te liczby mieszane. Na przykład ułamek dziesiętny 56,002 odpowiada liczbie mieszanej, dlatego ułamek dziesiętny 56,002 jest odczytywany jako „pięćdziesiąt sześć przecinek dwie tysięczne”.

Miejsca w ułamkach dziesiętnych

W notacji dziesiętnej, a także w notacji liczby naturalne, znaczenie każdej cyfry zależy od jej pozycji. Rzeczywiście, liczba 3 w dziesiętnym 0,3 oznacza trzy dziesiąte, w dziesiętnym 0,0003 - trzy dziesięć tysięcznych, a dziesiętnie 30.000,152 - trzy dziesiątki tysięcy. W ten sposób możemy mówić o cyfry dziesiętne, a także o cyfrach w liczbach naturalnych.

Nazwy cyfr w ułamku dziesiętnym do kropki dziesiętnej całkowicie pokrywają się z nazwami cyfr w liczbach naturalnych. A nazwy cyfr w ułamku dziesiętnym po przecinku są widoczne z poniższej tabeli.

Na przykład w ułamku dziesiętnym 37,051 liczba 3 jest na miejscu dziesiątek, 7 na miejscu jednostek, 0 na miejscu dziesiątym, 5 na miejscu setnym, 1 na miejscu tysięcznym.

Cyfry w ułamku dziesiętnym różnią się również starszeństwem. Jeśli przejdziemy od cyfry do cyfry od lewej do prawej w zapisie dziesiętnym, to przejdziemy od senior do młodsze stopnie. Na przykład cyfra setek jest starsza niż cyfra dziesiątych, a cyfra milionowych jest młodsza niż cyfra setnych. W tym ostatnim ułamku dziesiętnym możemy mówić o najbardziej znaczącej i najmniej znaczącej cyfrze. Na przykład w postaci dziesiętnej 604.9387 senior (najwyższy) cyfra to cyfra setek i młodszy (najniższy)- miejsce dziesięciotysięczne.

W przypadku ułamków dziesiętnych następuje ekspansja na cyfry. Jest to podobne do ekspansji cyfr liczb naturalnych. Na przykład rozszerzenie dziesiętne 45.6072 to: 45.6072=40+5+0.6+0.007+0.0002 . A właściwości dodawania z rozwinięcia ułamka dziesiętnego na cyfry pozwalają przejść do innych reprezentacji tego ułamka dziesiętnego, na przykład 45,6072=45+0,6072 , lub 45,6072=40,6+5,007+0,0002 , lub 45,6072= 45,0072+0,6 .

Końcowe ułamki dziesiętne

Do tego momentu mówiliśmy tylko o ułamkach dziesiętnych, w których zapisie znajduje się skończona liczba cyfr po przecinku. Takie ułamki nazywane są skończonymi ułamkami dziesiętnymi.

Definicja.

Końcowe ułamki dziesiętne- Są to ułamki dziesiętne, których rekordy zawierają skończoną liczbę znaków (cyfr).

Oto kilka przykładów ostatnich miejsc po przecinku: 0,317 , 3,5 , 51.1020304958 , 230 032,45 .

Jednak nie każdy wspólny ułamek może być reprezentowany jako ułamek skończony dziesiętny. Na przykład ułamek 5/13 nie może być zastąpiony równym ułamkiem z jednym z mianowników 10, 100, ..., dlatego nie można go przekonwertować na ostatni ułamek dziesiętny. Porozmawiamy o tym więcej w części poświęconej teorii konwersji zwykłych ułamków zwykłych na ułamki dziesiętne.

Nieskończone ułamki dziesiętne: ułamki okresowe i nieokresowe

W zapisie ułamka dziesiętnego po przecinku można dopuścić nieskończoną liczbę cyfr. W tym przypadku przejdziemy do rozważenia tak zwanych nieskończonych ułamków dziesiętnych.

Definicja.

Nieskończone ułamki dziesiętne- Są to ułamki dziesiętne, w których zapisie jest nieskończona ilość cyfr.

Oczywiste jest, że nie możemy zapisać nieskończonych ułamków dziesiętnych w całości, dlatego w ich zapisie ograniczają się one tylko do pewnej skończonej liczby cyfr po przecinku i umieszczają wielokropek wskazujący nieskończenie ciągły ciąg cyfr. Oto kilka przykładów nieskończonych ułamków dziesiętnych: 0.143940932…, 3.1415935432…, 153.02003004005…, 2.111111111…, 69.74152152152….

Jeśli przyjrzysz się uważnie ostatnim dwóm nieskończonym ułamkom dziesiętnym, to w ułamku 2.111111111 ... nieskończenie powtarzająca się liczba 1 jest wyraźnie widoczna, aw ułamku 69.74152152152 ..., zaczynając od trzeciego miejsca po przecinku, powtarzająca się grupa liczb 1, 5 i 2 są wyraźnie widoczne. Takie nieskończone ułamki dziesiętne nazywane są okresowymi.

Definicja.

Okresowe ułamki dziesiętne(lub po prostu ułamki okresowe ) to nieskończone ułamki dziesiętne, w zapisie których począwszy od określonego miejsca dziesiętnego, pewna cyfra lub grupa cyfr, która nazywa się okres ułamkowy.

Na przykład okres ułamka okresowego 2.111111111... to liczba 1, a okres ułamka okresowego 69.74152152152... to grupa liczb, np. 152.

Dla nieskończonych okresowych ułamków dziesiętnych przyjęto specjalny zapis. Dla zwięzłości zgodziliśmy się napisać kropkę raz, umieszczając ją w nawiasach. Na przykład ułamek okresowy 2.111111111… jest zapisany jako 2,(1) , a ułamek okresowy 69.74152152152… jest zapisany jako 69.74(152) .

Warto zauważyć, że dla tego samego okresowego ułamka dziesiętnego można określić różne okresy. Na przykład ułamek dziesiętny okresu 0,73333… można uznać za ułamek dziesiętny 0,7(3) z okresem 3, ułamek dziesiętny 0,7(33) z okresem 33 itd. 0,7(333), 0,7 (3333 ), ... Możesz również spojrzeć na ułamek okresowy 0,73333 ... tak: 0.733(3) , lub tak 0,73(333), itd. Tutaj, aby uniknąć niejasności i niespójności, zgadzamy się, aby za okres ułamka dziesiętnego uznać najkrótszy ze wszystkich możliwych ciągów powtarzających się cyfr, zaczynając od najbliższej pozycji do kropki dziesiętnej. Oznacza to, że okres ułamka dziesiętnego 0,73333… będzie uważany za ciąg jednej cyfry 3, a częstotliwość zaczyna się od drugiej pozycji po przecinku, czyli 0,73333…=0,7(3) . Inny przykład: ułamek okresowy 4.7412121212… ma okres 12, okresowość zaczyna się od trzeciej cyfry po przecinku, czyli 4.7412121212…=4.74(12) .

Nieskończone dziesiętne ułamki okresowe są uzyskiwane poprzez konwersję na ułamki dziesiętne zwykłych ułamków, których mianowniki zawierają czynniki pierwsze, inny niż 2 i 5.

Tutaj warto wspomnieć o ułamkach okresowych z okresem 9. Oto przykłady takich ułamków: 6.43(9) , 27,(9) . Te ułamki są kolejnym zapisem ułamków okresowych z okresem 0 i zwyczajowo zastępuje się je ułamkami okresowymi z okresem 0. W tym celu okres 9 zastępuje się okresem 0, a wartość kolejnej najwyższej cyfry zwiększa się o jeden. Na przykład ułamek z okresem 9 w postaci 7.24(9) jest zastępowany ułamkiem okresowym z okresem 0 w postaci 7.25(0) lub równym końcowym ułamkiem dziesiętnym równym 7.25. Inny przykład: 4,(9)=5,(0)=5 . Równość ułamka z okresem 9 i odpowiedniego ułamka z okresem 0 można łatwo ustalić po zastąpieniu tych ułamków dziesiętnych ich równymi zwykłymi ułamkami.

Na koniec przyjrzyjmy się bliżej nieskończonym liczbom dziesiętnym, które nie mają nieskończenie powtarzającej się sekwencji cyfr. Nazywa się je nieokresowymi.

Definicja.

Jednorazowe ułamki dziesiętne(lub po prostu ułamki nieokresowe) to nieskończone liczby dziesiętne bez kropki.

Czasami ułamki nieokresowe mają postać podobną do ułamków okresowych, na przykład 8.02002000200002 ... jest ułamkiem nieokresowym. W takich przypadkach należy szczególnie uważać, aby zauważyć różnicę.

Zauważ, że ułamki nieokresowe nie są konwertowane na zwykłe ułamki, nieskończone nieokresowe ułamki dziesiętne reprezentują liczby niewymierne.

Operacje z ułamkami dziesiętnymi

Jedną z czynności z ułamkami dziesiętnymi jest porównanie, a także zdefiniowano cztery podstawowe działania arytmetyczne operacje na ułamkach dziesiętnych: dodawanie, odejmowanie, mnożenie i dzielenie. Rozważ osobno każdą z akcji z ułamkami dziesiętnymi.

Porównanie dziesiętne zasadniczo na podstawie porównania zwykłych ułamków zwykłych odpowiadających porównywanym ułamkom dziesiętnym. Jednak konwersja ułamków dziesiętnych na zwykłe jest dość czasochłonną operacją, a nieskończone ułamki nieokresowe nie mogą być reprezentowane jako zwykły ułamek, więc wygodnie jest używać bitowego porównania ułamków dziesiętnych. Bitowe porównywanie liczb dziesiętnych jest podobne do porównywania liczb naturalnych. Aby uzyskać bardziej szczegółowe informacje, zalecamy przestudiowanie porównania materiałów artykułu ułamków dziesiętnych, reguł, przykładów, rozwiązań.

Przejdźmy do następnego kroku - mnożenie ułamków dziesiętnych. Mnożenie końcowych ułamków dziesiętnych odbywa się podobnie jak odejmowanie ułamków dziesiętnych, zasady, przykłady, rozwiązania mnożenia przez kolumnę liczb naturalnych. W przypadku ułamków okresowych mnożenie można sprowadzić do mnożenia ułamków zwykłych. Z kolei mnożenie nieskończonych nieokresowych ułamków dziesiętnych po ich zaokrągleniu sprowadza się do mnożenia skończonych ułamków dziesiętnych. Zalecamy dalsze przestudiowanie materiału artykułu mnożenie ułamków dziesiętnych, reguły, przykłady, rozwiązania.

Ułamki dziesiętne na wiązce współrzędnych

Między kropkami i ułamkami dziesiętnymi istnieje zależność jeden do jednego.

Zastanówmy się, jak konstruowane są punkty na promieniu współrzędnych odpowiadającym danemu ułamkowi dziesiętnemu.

Możemy zastąpić skończone ułamki dziesiętne i nieskończone okresowe ułamki dziesiętne zwykłymi ułamkami równymi im, a następnie skonstruować odpowiadające im zwykłe ułamki na promieniu współrzędnych. Na przykład ułamek dziesiętny 1,4 odpowiada zwykłemu ułamkowi 14/10, dlatego punkt o współrzędnej 1,4 jest usuwany z początku w kierunku dodatnim o 14 segmentów równych jednej dziesiątej jednego segmentu.

Ułamki dziesiętne można zaznaczyć na wiązce współrzędnych, zaczynając od rozwinięcia tego ułamka dziesiętnego na cyfry. Na przykład powiedzmy, że musimy zbudować punkt o współrzędnej 16.3007 , ponieważ 16.3007=16+0.3+0.0007 , wtedy możemy dostać się do tego punktu układając kolejno 16 odcinków jednostkowych od początku współrzędnych, 3 odcinki, długość z czego równa się jednej dziesiątej jednostki oraz 7 segmentów, których długość jest równa jednej dziesiątej części jednostki.

Ta metoda konstruowania liczb dziesiętnych na wiązce współrzędnych pozwala zbliżyć się tak blisko, jak chcesz, do punktu odpowiadającego nieskończonemu ułamkowi dziesiętnemu.

Czasami możliwe jest dokładne wykreślenie punktu odpowiadającego nieskończonej liczbie dziesiętnej. Na przykład, , to ten nieskończony ułamek dziesiętny 1.41421... odpowiada punktowi współrzędnej, oddalonemu od początku o długość przekątnej kwadratu o boku 1 jednostki segmentu.

Odwrotny proces uzyskiwania ułamka dziesiętnego odpowiadającego danemu punktowi na wiązce współrzędnych to tzw dziesiętny pomiar segmentu. Zobaczmy, jak to się robi.

Niech naszym zadaniem będzie dostanie się od początku do danego punktu na linii współrzędnych (lub nieskończone zbliżenie się do niego, jeśli nie można się do niego dostać). Przy pomiarze dziesiętnym odcinka możemy sukcesywnie odkładać dowolną ilość jednostkowych odcinków od początku, następnie odcinków o długości równej jednej dziesiątej jednego odcinka, od odcinków o długości równej jednej setnej odcinka itd. . Zapisując liczbę wykreślonych odcinków o każdej długości otrzymujemy ułamek dziesiętny odpowiadający danemu punktowi na promieniu współrzędnych.

Na przykład, aby dostać się do punktu M na powyższym rysunku, musisz odłożyć 1 segment jednostki i 4 segmenty, których długość jest równa dziesiątej części jednostki. Zatem punkt M odpowiada ułamkowi dziesiętnemu 1,4.

Oczywiste jest, że punkty wiązki współrzędnych, do których nie można dotrzeć podczas pomiaru dziesiętnego, odpowiadają nieskończonym ułamkom dziesiętnym.

Bibliografia.

Matematyka: studia. na 5 komórek. ogólne wykształcenie instytucje / N. Ya Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21. ed., wymazane. - M.: Mnemosyne, 2007. - 280 s.: ch. ISBN 5-346-00699-0.
Matematyka. Klasa 6: podręcznik. dla kształcenia ogólnego instytucje / [N. Ya Vilenkin i inni]. - wyd. 22, ks. - M.: Mnemosyne, 2008. - 288 s.: chor. ISBN 978-5-346-00897-2.
Algebra: podręcznik na 8 ogniw. ogólne wykształcenie instytucje / [Ju. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; wyd. S. A. Teliakowski. - 16 wyd. - M. : Edukacja, 2008. - 271 s. : chory. - ISBN 978-5-09-019243-9.
Gusiew V.A., Mordkovich A.G. Matematyka (podręcznik dla kandydatów do szkół technicznych): Proc. dodatek.- M.; Wyższy szkoła, 1984.-351 s., chor.

Jak wiadomo, zbiór liczb wymiernych (Q) zawiera zbiór liczb całkowitych (Z), który z kolei zawiera zbiór liczb naturalnych (N). Oprócz liczb całkowitych liczby wymierne obejmują ułamki.

Dlaczego zatem cały zbiór liczb wymiernych jest czasami uważany za nieskończone dziesiętne ułamki okresowe? Rzeczywiście, oprócz ułamków obejmują liczby całkowite, a także ułamki nieokresowe.

Faktem jest, że wszystkie liczby całkowite, jak również każdy ułamek, mogą być reprezentowane jako nieskończony okresowy ułamek dziesiętny. Oznacza to, że dla wszystkich liczb wymiernych możesz użyć tej samej notacji.

Jak jest reprezentowana nieskończona okresowa liczba dziesiętna? W nim powtarzająca się grupa liczb po przecinku jest ujęta w nawiasy. Na przykład 1.56(12) to ułamek, w którym powtarza się grupa cyfr 12, czyli ułamek ma wartość 1.561212121212...i tak dalej bez końca. Powtarzająca się grupa cyfr nazywana jest kropką.

Jednak w podobnej formie możemy przedstawić dowolną liczbę, jeśli weźmiemy pod uwagę liczbę 0 jako jej okres, który również powtarza się bez końca. Na przykład liczba 2 jest taka sama jak 2,0000... Dlatego można ją zapisać jako nieskończony ułamek okresowy, tj. 2,(0).

To samo można zrobić z dowolną skończoną frakcją. Na przykład:

0,125 = 0,1250000... = 0,125(0)

Jednak w praktyce nie stosuje się przekształcenia ułamka skończonego w nieskończony ułamek okresowy. Dlatego rozdzielane są ułamki skończone i ułamki nieskończone okresowe. W związku z tym bardziej poprawne jest stwierdzenie, że liczby wymierne obejmują

wszystkie liczby całkowite,
frakcje końcowe,
nieskończone ułamki okresowe.

Jednocześnie po prostu pamiętają, że liczby całkowite i ułamki skończone mogą być teoretycznie reprezentowane jako nieskończone ułamki okresowe.

Z drugiej strony pojęcia ułamków skończonych i nieskończonych mają zastosowanie do ułamków dziesiętnych. Jeśli mówimy o zwykłych ułamkach zwykłych, to zarówno skończone, jak i nieskończone ułamki dziesiętne mogą być jednoznacznie reprezentowane jako zwykły ułamek. Tak więc z punktu widzenia ułamków zwykłych ułamki okresowe i skończone są jednym i tym samym. Ponadto liczby całkowite mogą być również reprezentowane jako wspólny ułamek, jeśli wyobrazimy sobie, że dzielimy tę liczbę przez 1.

Jak przedstawić dziesiętny nieskończony ułamek okresowy w postaci zwykłego? Najczęściej stosowanym algorytmem jest:

Doprowadzają ułamek do postaci, aby po przecinku była tylko kropka.
Pomnóż nieskończony ułamek okresowy przez 10 lub 100 lub ... tak, aby przecinek przesunął się w prawo o jeden okres (to znaczy, że jeden okres znajduje się w części całkowitej).
Pierwotny ułamek (a) jest utożsamiany ze zmienną x, a ułamek (b) otrzymany przez pomnożenie przez liczbę N jest równy Nx.
Odejmij x od Nx. Odejmij a od b. Oznacza to, że tworzą równanie Nx - x \u003d b - a.
Podczas rozwiązywania równania otrzymuje się zwykły ułamek.

Przykład konwersji nieskończonego okresowego ułamka dziesiętnego na zwykły ułamek:
x = 1.13333...
10x = 11,3333...
10x * 10 = 11.33333... * 10
100x = 113,3333...
100x – 10x = 113,3333... – 11,3333...
90x=102
x=

Aby zapisać liczbę wymierną m / n jako ułamek dziesiętny, musisz podzielić licznik przez mianownik. W tym przypadku iloraz jest zapisany jako ułamek skończony lub nieskończony dziesiętny.

oparzenie podany numer jako ułamek dziesiętny.

Rozwiązanie. Podziel licznik każdego ułamka przez jego mianownik: ale) podziel 6 przez 25; b) podziel 2 przez 3; w) dzielimy 1 przez 2, a następnie dodajemy otrzymany ułamek do jednego - całkowitej części tej liczby mieszanej.

Nierozkładalne zwykłe ułamki, których mianowniki nie zawierają dzielników pierwszych innych niż 2 I 5 , są zapisywane jako ostatni ułamek dziesiętny.

W Przykład 1 gdy ale) mianownik 25=5 5; gdy w) mianownik to 2, więc otrzymaliśmy ostatnie ułamki dziesiętne 0,24 i 1,5. Kiedy b) mianownik to 3, więc wynik nie może być zapisany jako ostatnia liczba dziesiętna.

Czy można bez podziału na kolumnę zamienić taki zwykły ułamek na ułamek dziesiętny, którego mianownik nie zawiera innych dzielników, z wyjątkiem 2 i 5? Wymyślmy to! Jaki ułamek nazywa się dziesiętnym i jest zapisywany bez linii ułamkowej? Odpowiedź: ułamek z mianownikiem 10; sto; 1000 itd. I każda z tych liczb to produkt równy liczba dwójek i piątki. Właściwie: 10=2 5 ; 100=2 5 2 5 ; 1000=2 5 2 5 2 5 itd.

Dlatego mianownik nieredukowalnego zwykłego ułamka będzie musiał być przedstawiony jako iloczyn „dwójek” i „piątek”, a następnie pomnożony przez 2 i (lub) przez 5, aby „dwójki” i „piątki” stały się równe. Wtedy mianownik ułamka będzie równy 10 lub 100 lub 1000 itd. Aby wartość ułamka się nie zmieniła, mnożymy licznik ułamka przez tę samą liczbę, przez którą pomnożono mianownik.

Wyraź następujące ułamki zwykłe jako ułamki dziesiętne:

Rozwiązanie. Każda z tych frakcji jest nieredukowalna. Rozłóżmy mianownik każdego ułamka na czynniki pierwsze.

20=2 2 5. Wniosek: brakuje jednej „piątki”.

8=2 2 2. Wniosek: brakuje trzech „piątek”.

25=5 5. Wniosek: brakuje dwóch „dwójek”.

Komentarz. W praktyce często nie stosują faktoryzacji mianownika, ale po prostu zadają pytanie: o ile należy pomnożyć mianownik, aby wynik był jednostką z zerami (10 lub 100 lub 1000 itd.). A następnie licznik mnoży się przez tę samą liczbę.

Więc na wypadek ale)(przykład 2) z liczby 20 możesz otrzymać 100 mnożąc przez 5, dlatego musisz pomnożyć licznik i mianownik przez 5.

Kiedy b)(przykład 2) z liczby 8 liczba 100 nie zadziała, ale liczbę 1000 uzyskamy mnożąc przez 125. Zarówno licznik (3), jak i mianownik (8) ułamka są pomnożone przez 125.

Kiedy w)(przykład 2) na 25 otrzymasz 100 po pomnożeniu przez 4. Oznacza to, że licznik 8 również musi zostać pomnożony przez 4.

Nieskończony ułamek dziesiętny, w którym jedna lub więcej cyfr niezmiennie powtarza się w tej samej kolejności, nazywa się czasopismo Ułamek dziesiętny. Zbiór powtarzających się cyfr nazywa się okresem tego ułamka. Dla zwięzłości kropkę ułamka zapisuje się raz, umieszczając go w nawiasach.

Kiedy b)(przykład 1 ) powtarzająca się cyfra to jeden i równa się 6. Zatem nasz wynik 0,66... będzie zapisany tak: 0,(6) . Czytali: zero liczb całkowitych, sześć w okresie.

Jeśli między przecinkiem a pierwszym okresem jest co najmniej jedna cyfra jednorazowa, taki ułamek okresowy nazywa się mieszanym ułamkiem okresowym.

Nieredukowalny zwykły ułamek, którego mianownik razem z innymi mnożnik zawiera mnożnik 2 lub 5 , staje się mieszany ułamek okresowy.

Zapisz liczbę jako ułamek dziesiętny:

Dowolną liczbę wymierną można zapisać jako nieskończony okresowy ułamek dziesiętny.

Zapisz liczbę jako nieskończony ułamek okresowy.

Nieskończone ułamki dziesiętne

Ułamki dziesiętne po przecinku mogą zawierać nieskończoną liczbę cyfr.

Nieskończone ułamki dziesiętne-- To są ułamki dziesiętne, w zapisie których jest nieskończona liczba cyfry.

Nieskończony ułamek dziesiętny jest prawie niemożliwy do całkowitego zapisania, dlatego podczas ich zapisywania ograniczają się tylko do pewnej skończonej liczby cyfr po przecinku, po czym umieszczają wielokropek, co wskazuje na nieskończenie ciągłą sekwencję cyfr.

Przykład 1

Na przykład $0.443340831\dots ; 3.1415935432\kropki ; 135,126730405\kropki ; 4.333333333333\kropki ; 676.68349349\kropki$.

Rozważ dwa ostatnie nieskończone miejsca po przecinku. W ułamku $4.3333333333\dots$ cyfra $3$ powtarza się w nieskończoność, a we ułamku $676.68349349\dots$ grupa cyfr $3$, $4$ i $9$ powtarza się od trzeciego miejsca po przecinku. Takie nieskończone ułamki dziesiętne nazywane są okresowymi.

Okresowe ułamki dziesiętne

Okresowe ułamki dziesiętne(lub ułamki okresowe) to nieskończone ułamki dziesiętne, w zapisie których, od pewnego znaku po przecinku, pewna cyfra lub ich grupa, którą nazywamy okresem ułamka, powtarza się w nieskończoność.

Przykład 2

Na przykład, okres ułamka okresowego $4.333333333333\dots$ to cyfra $3$, a okres ułamka $676.68349349\dots$ to grupa cyfr $349$.

Dla zwięzłości pisania nieskończonych okresowych ułamków dziesiętnych zwyczajowo zapisuje się kropkę raz, umieszczając ją w nawiasach. Na przykład ułamek okresowy $4.33333333333\dots$ zapisywany jest w $4,(3)$, a ułamek okresowy $676.68349349\dots$ zapisywany jest $676.68(349)$.

Nieskończone ułamki dziesiętne okresowe są uzyskiwane przez konwersję zwykłych ułamków, których mianowniki zawierają czynniki pierwsze inne niż 2$ i 5$ na ułamki dziesiętne.

Dowolny skończony ułamek dziesiętny (i liczbę całkowitą) można zapisać jako ułamek okresowy, dla którego wystarczy dodać nieskończoną liczbę cyfr $0$ po prawej stronie.

Przykład 3

Na przykład, skończony dziesiętny 45,12$ może być zapisany jako ułamek okresowy jako 45,12(0)$, a liczba całkowita $(74)$ jako nieskończona okresowa liczba dziesiętna to 74(0)$.

W przypadku ułamków okresowych, które mają okres 9, użyj przejścia do innej notacji ułamka okresowego z okresem 0$. Tylko w tym celu okres 9 zostaje zastąpiony okresem 0$, a wartość kolejnej największej cyfry wzrasta o 1$.

Przykład 4

Na przykład ułamek okresowy 7,45(9)$ może zostać zastąpiony ułamkiem okresowym 7,46(0)$ lub równym ułamkiem dziesiętnym 7,46$.

Nieskończone dziesiętne ułamki okresowe są reprezentowane przez liczby wymierne. Innymi słowy, każdy ułamek okresowy może zostać przekonwertowany na ułamek wspólny, a każdy ułamek wspólny może być reprezentowany jako ułamek okresowy.

Konwersja zwykłych ułamków zwykłych na skończone i nieskończone okresowe ułamki dziesiętne

Nie tylko zwykłe ułamki zwykłe z mianownikami $10, 100, \dots$ mogą być konwertowane na dziesiętne.

W niektórych przypadkach pierwotny wspólny ułamek można łatwo zredukować do mianownika 10$, 100$ lub 1\000$, po czym wynikowy ułamek można przedstawić jako ułamek dziesiętny.

Przykład 5

Aby zredukować ułamek $\frac(3)(5)$ do ułamka z mianownikiem $10$, należy pomnożyć licznik i mianownik ułamka przez $2$, po czym otrzymamy $\frac(6)(10) $, co nie jest trudne do przetłumaczenia na dziesiętne 0,6 $.

W innych przypadkach stosuje się inny sposób zamiany zwykłego ułamka na ułamek dziesiętny:

licznik należy zastąpić ułamkiem dziesiętnym z dowolną liczbą zer po przecinku;

podziel licznik ułamka przez mianownik (podział wykonuje się jako podział liczb naturalnych na kolumnę, a w ilorazu wstawiamy kropkę dziesiętną po zakończeniu dzielenia części całkowitej dywidendy).

Przykład 6

Konwertuj ułamek zwykły $\frac(621)(4)$ na dziesiętny.

Rozwiązanie.

Zaprezentujmy liczbę $621$ w liczniku jako ułamek dziesiętny. Aby to zrobić, dodaj kropkę dziesiętną i na początek dwa zera po nim. Ponadto, jeśli to konieczne, możesz dodać więcej zer. Tak więc otrzymaliśmy 621,00 $.

Podzielmy liczbę 621,00 $ przez 4 $ w kolumnie:

Obrazek 1.

Podział osiągnął punkt dziesiętny w dywidendzie, a reszta nie wynosi zero. W tym przypadku kropka dziesiętna jest umieszczana w ilorazie, a dzielenie jest kontynuowane o kolumnę, niezależnie od przecinków:

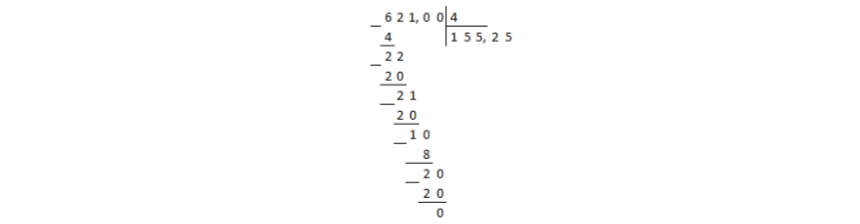
Rysunek 2.

Reszta to zero, co oznacza, że podział się skończył.

Odpowiedź: $155,25$.

Przypadek jest możliwy, gdy dzielenie licznika i mianownika zwykłego ułamka w pozostałej części $0 nie działa. W takim przypadku podział może być kontynuowany w nieskończoność. Począwszy od pewnego momentu, resztki dzielenia powtarzają się cyklicznie, co oznacza, że liczby w ilorazie również się powtarzają. Z tego możemy wywnioskować, że ten zwykły ułamek zostanie przetłumaczony na nieskończony okresowy ułamek dziesiętny.

Przykład 7

Zamień ułamek zwykły $\frac(19)(44)$ na ułamek dziesiętny.

Rozwiązanie.)

Aby zamienić zwykły ułamek zwykły na ułamek dziesiętny, dokonujemy podziału na kolumnę:

Rysunek 3

Dzielenie powtarza reszty 8$ i 36$, a iloraz powtarza również cyfry 1$ i 8$. Tak więc pierwotny ułamek zwykły $\frac(19)(44)$ został przekonwertowany na ułamek okresowy $\frac(19)(44)=0.43181818\dots =0.43(18)$.

Odpowiedź: $0,43(18)$.

Ogólny wniosek dotyczący zamiany zwykłych ułamków zwykłych na ułamki dziesiętne:

jeśli mianownik można rozłożyć na czynniki pierwsze, wśród których będą obecne tylko liczby 2$ i 5$, to taki ułamek można przeliczyć na końcowy ułamek dziesiętny;

jeśli oprócz liczb $2$ i $5$ w rozwinięciu mianownika są jeszcze inne liczby liczby pierwsze, wtedy taki ułamek jest tłumaczony na nieskończony ułamek dziesiętny okresowy.

Pamiętasz, jak w pierwszej lekcji o ułamkach dziesiętnych powiedziałem, że istnieją ułamki numeryczne, których nie można przedstawić jako ułamki dziesiętne (patrz lekcja „Ułamki dziesiętne”)? Dowiedzieliśmy się również, jak rozkładać na czynniki mianowniki ułamki, aby sprawdzić, czy istnieją liczby inne niż 2 i 5.

A więc: skłamałem. A dzisiaj dowiemy się, jak przetłumaczyć absolutnie dowolny ułamek liczbowy na ułamek dziesiętny. Jednocześnie zapoznamy się z całą klasą ułamków o nieskończenie znaczącej części.

Cykliczny dziesiętny to dowolny dziesiętny, który ma:

Część znacząca składa się z nieskończonej liczby cyfr;

W określonych odstępach czasu powtarzają się liczby w części znaczącej.

Zestaw powtarzających się cyfr, które tworzą znaczna część, nazywana jest okresową częścią ułamka, a liczba cyfr w tym zestawie to okres ułamka. Pozostały odcinek części znaczącej, który się nie powtarza, nazywa się częścią nieokresową.

Ponieważ definicji jest wiele, warto szczegółowo rozważyć kilka z tych ułamków:

Ta frakcja występuje najczęściej w problemach. Część nieokresowa: 0; część okresowa: 3; długość okresu: 1.

Część nieokresowa: 0,58; część okresowa: 3; długość okresu: ponownie 1.

Część nieokresowa: 1; część okresowa: 54; długość okresu: 2.

Część nieokresowa: 0; część okresowa: 641025; długość okresu: 6. Dla wygody powtarzające się części są oddzielone od siebie spacją – w tym rozwiązaniu nie jest to konieczne.

Część nieokresowa: 3066; część okresowa: 6; długość okresu: 1.

Jak widać, definicja ułamka okresowego opiera się na pojęciu znaczna część liczby. Dlatego jeśli zapomniałeś, co to jest, polecam to powtórzyć - zobacz lekcję „”.

Przejście do okresowego dziesiętnego

Rozważ zwykły ułamek postaci a/b. Rozłóżmy jego mianownik na proste czynniki. Istnieją dwie opcje:

W rozszerzeniu obecne są tylko dzielniki 2 i 5. Te ułamki można łatwo sprowadzić do postaci dziesiętnych - patrz lekcja „Ułamki dziesiętne”. Nie jesteśmy tym zainteresowani;
W rozszerzeniu jest coś jeszcze oprócz 2 i 5. W tym przypadku ułamek nie może być przedstawiony jako ułamek dziesiętny, ale można go przekształcić w ułamek dziesiętny okresowy.

Aby ustawić okresowy ułamek dziesiętny, musisz znaleźć jego okresową i nieokresową część. W jaki sposób? Zamień ułamek na ułamek niewłaściwy, a następnie podziel licznik przez mianownik z „rogem”.

W ten sposób nastąpią następujące zdarzenia:

Najpierw dziel cała część jeśli istnieje;
Po przecinku może być kilka liczb;
Po chwili zaczną się numery powtarzać.

To wszystko! Cyfry powtarzające się po przecinku są oznaczane przez część okresową, a to, co jest przed - nieokresowe.

Zadanie. Konwertuj zwykłe ułamki zwykłe na okresowe ułamki dziesiętne:

Wszystkie ułamki bez części całkowitej, więc po prostu dzielimy licznik przez mianownik z „rogem”:

Jak widać, pozostałości się powtarzają. Zapiszmy ułamek w „poprawnej” postaci: 1,733 ... = 1,7(3).

Wynik jest ułamkiem: 0,5833 ... = 0,58(3).

Piszemy w postaci normalnej: 4.0909 ... = 4, (09).

Otrzymujemy ułamek: 0,4141 ... = 0, (41).

Przejście od okresowego dziesiętnego do zwykłego

Rozważmy okres dziesiętny X = abc (a 1 b 1 c 1). Wymagane jest przeniesienie go do klasycznego „dwupiętrowego”. Aby to zrobić, wykonaj cztery proste kroki:

Znajdź okres ułamka, tj. policz, ile cyfr znajduje się w części okresowej. Niech to będzie liczba k;
Znajdź wartość wyrażenia X · 10 k . Odpowiada to przesunięciu kropki dziesiętnej o pełny okres w prawo - patrz lekcja " Mnożenie i dzielenie ułamków dziesiętnych";
Odejmij oryginalne wyrażenie od otrzymanej liczby. W tym przypadku część okresowa jest „wypalona” i pozostaje wspólny ułamek;
Znajdź X w otrzymanym równaniu. Wszystkie ułamki dziesiętne są konwertowane na zwykłe.

Zadanie. Zamień na zwykły niewłaściwy ułamek liczby:

9,(6);
32,(39);
0,30(5);
0,(2475).

Praca z pierwszym ułamkiem: X = 9,(6) = 9,666...

Nawiasy zawierają tylko jedną cyfrę, więc okres k = 1. Następnie mnożymy ten ułamek przez 10 k = 10 1 = 10. Mamy:

10X = 10 9,6666... = 96,666...

Odejmij pierwotny ułamek i rozwiąż równanie:

10X - X = 96,666 ... - 9,666 ... = 96 - 9 = 87;
9X=87;
X = 87/9 = 29/3.

Zajmijmy się teraz drugą frakcją. Więc X = 32,(39) = 32,393939...

Okres k = 2, więc mnożymy wszystko przez 10 k = 10 2 = 100:

100X = 100 32,393939 ... = 3239,3939 ...

Odejmij ponownie pierwotny ułamek i rozwiąż równanie:

100X - X = 3239,3939 ... - 32,3939 ... = 3239 - 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.

Przejdźmy do trzeciego ułamka: X = 0,30(5) = 0,30555 ... Schemat jest taki sam, więc podam tylko obliczenia:

Okres k = 1 ⇒ pomnóż wszystko przez 10 k = 10 1 = 10;

10X = 10 0,30555... = 3,05555...
10X - X = 3,0555 ... - 0,305555 ... = 2,75 = 11/4;
9X = 11/4;
X = (11/4) : 9 = 11/36.

Wreszcie ostatni ułamek: X = 0,(2475) = 0,2475 2475... Ponownie dla wygody części okresowe są oddzielone od siebie spacjami. Mamy:

k = 4 ⇒ 10 k = 10 4 = 10 000;
10 000X = 10 000 0,2475 2475 = 2475,2475 ...
10 000X - X = 2475,2475 ... - 0,2475 2475 ... = 2475;
9999X = 2475;
X = 2475: 9999 = 25/101.